La gravedad newtoniana de una fuente puntual se puede describir mediante un potencial $ \ Phi = - \ mu / r $. Si suprimimos una dimensión espacial y la usamos para graficar el valor de este potencial, obtenemos algo que se parece mucho a esta ilustración y, de hecho, es infinitamente profundo en el centro, al menos en la idealización de un punto-masa. . Y más lejos del centro, se vuelve plano, tal como lo tienen muchas ilustraciones como esta.
Ilustraciones como esta son bastante comunes, y supongo que, en última instancia, están inspiradas en el potencial newtoniano, porque no tienen casi nada que ver con la curvatura del espacio-tiempo.
Aquí hay una incrustación isométrica de la geometría de Schwarzschild en un instante del tiempo de Schwarzschild, nuevamente con una dimensión suprimida:
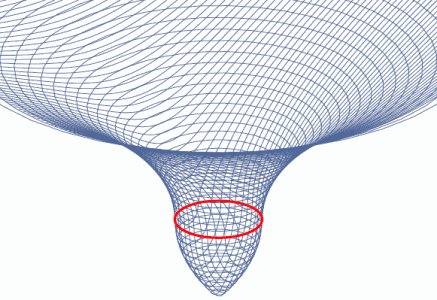
Por encima del horizonte (círculo rojo), la superficie es una parte de un paraboloide (el paraboloide Flamm ). A diferencia del potencial, no se aplana a grandes distancias.
Ser isométrico significa que representa correctamente las distancias espaciales sobre el horizonte en un instante del tiempo de Schwarzschild. Debajo del horizonte, la incrustación no es técnicamente precisa porque la coordenada radial de Schwarzschild no representa el espacio allí, sino el tiempo. Aunque si pretendemos que es como un espacio debajo del horizonte, esa sería la incrustación correcta. Imagine que la parte debajo del horizonte tiene un flujo unidireccional hacia la singularidad.
Dado que solo hemos representado el espacio y no el tiempo, la incrustación no es suficiente para reconstruir las trayectorias de las partículas en este espacio-tiempo. Aún así, es una representación más precisa de una parte de la curvatura espacio-temporal de la fuente puntual, específicamente la parte espacial.
La velocidad del objeto desde esta perspectiva, parecería aumentar, hasta un punto - donde la velocidad en las coordenadas x, y comienza a disminuir debido a que la mayor parte del movimiento ocurre "hacia abajo" en la dimensión del tiempo. ¿Esto también es correcto? ¿Parecería que un fotón se ralentiza al moverse por el pozo, si se ve desde arriba?
Lo anterior es una incrustación de una porción de geometría espacial, y no es un pozo de gravedad. La forma matemática del paraboloide sobre el horizonte se describe mejor en coordenadas cilíndricas como $$ r = 2M + \ frac {z ^ 2} {8M} \ text {.} $$ Aquí la vertical $ La coordenada z $ no significa nada físicamente. Es puramente un artefacto de crear una superficie de la misma curvatura intrínseca en el espacio euclidiano de $ 3 $ que la porción espacial de $ 2 $ -dimensional de la geometría de Schwarzschild.
Para el espacio-tiempo de Schwarzschild, la caída libre radial es en realidad exactamente newtoniana en la coordenada radial de Schwarzschild y el tiempo adecuado, es decir, el tiempo experimentado por el objeto en caída libre, en lugar del tiempo de Schwarzschild. Entonces, el pozo de gravedad newtoniano no es en realidad una mala imagen para la física, simplemente no es la geometría y, por lo tanto, no es una buena representación de cómo se curva cualquier parte del espacio-tiempo. Para las órbitas no radiales, el potencial efectivo es algo diferente al newtoniano, pero ignorar los efectos del momento angular nos da la forma newtoniana.
En el tiempo de Schwarzschild, sí, un fotón (o cualquier otra cosa ) disminuye la velocidad a medida que se acerca al horizonte. De hecho, en el tiempo de Schwarzschild nunca llega al horizonte, lo cual es una indicación de que las coordenadas de Schwarzschild se comportan mal en el horizonte. La aceleración de coordenadas en realidad se vuelve repulsiva cerca del horizonte y, para un objeto que cae lo suficientemente rápido, es siempre repulsiva. Esto puede entenderse como la partícula que se mueve hacia lugares con una dilatación del tiempo gravitacional cada vez mayor. Sin embargo, en el momento adecuado de cualquier observador en caída, cerca del horizonte la aceleración es siempre atractiva.